KMeans、LVQ、GaussianMixture几种聚类方法的Python实现以及标签映射(Kuhn-Munkres匈牙利算法)
字数统计:1030 阅读时长 ≈ 3分钟一、前言
KMeans、LVQ、GaussianMixture这几种方法都是非常经典的聚类算法,在机器学习中具有重要的地位。Python中有个sklearn的库,里面包含了大量的机器学习相关的方法,其中就包括了Kmeans和GaussianMixture这两种。
值得注意的是,在对每个算法实现之后,要对每个算法进行精确度的评价,这时候就用到了ACC和NMI这两个评价标准(具体是什么见后文),在评价时就需要用到标签的信息,但是在对数据进行聚类时,标签分配的规律与真实标签并不一定一致,所以就需要利用Kuhn-Munkres算法(匈牙利算法)来对预测的标签重排,而Python中也集成了Kuhn-Munkres算法。
二、利用Kuhn-Munkres算法映射标签的原理
假设真实数据标签为:{1,1,1,2,2,3,4,4,⋯,7,7,7,9,9}
而利用上述算法对数据聚类之后的标签可能是:{3,3,3,1,1,4,6,6,⋯,9,9,7,7,7}
就算在最理想的状态下,把所有该在一个簇中的数据都聚类到一个簇中,但是由于标签的规则不一致,所以每个簇给定的标号不一样。
这时候就需要利用到Kuhn-Munkres算法来对标签进行重新标号。
重新标号的主要思路就是,将聚类之后的每一种标签(称为预测标签)与每一种真实标签一一对比,计算出所有标签组合(i,j)情况的数据重合数量,这样就会形成一个“代价矩阵”,基于这个“代价矩阵”,就可以利用Kuhn-Munkres算法来找出代价最低的分配方式,也就是预测标签与真实标签之间的映射关系。
例如,现在具有以下数据(所有数据及代码下载方式见下文):
| 数据集 | 样本数 | 维度 | 类数 | 数据类型 |
|---|---|---|---|---|
| MINIST | 3000 | 784 | 10 | 手写体数字 |
| Yale | 165 | 1024 | 15 | 人脸图像 |
| lung | 203 | 3312 | 5 | 生物数据 |
对于数据lung.mat,具有5种标签,分别为{1,2,3,4,5},
所以预测标签与真实标签组合之后就会形成一个5×5的矩阵,矩阵中的每个值就代表该标签组合情况下数据的重合数量,例如

其中第1行第2列数字为38,就代表真实标签为1的数据与预测标签为2的数据重合的数量有38个,以此类推,计算此矩阵代码如下:
for i in range(nClass1):
ind_cla1 = L1 == Label1[i]
ind_cla1 = ind_cla1.astype(float)
for j in range(nClass2):
ind_cla2 = L2 == Label2[j]
ind_cla2 = ind_cla2.astype(float)
G[i, j] = np.sum(ind_cla2*ind_cla1)这里的代码如果对于Python不熟悉的话可能是比较难以理解的,但是这一部分的思想是真的巧妙,我也不知道怎么去详细解释,如果不懂的话就仔细看看Python中矩阵相关操作吧,尤其是numpy的了解非常重要。
上面我们得到了标签组合矩阵,但是Kuhn-Munkres算法是用来计算最低代价的分配方式的,(不了解Kuhn-Munkres算法的话建议去看这篇博客:Kuhn-Munkres算法将聚类后的预测标签映射为真实标签,如果不需要深究具体思路的,只需要了解这个算法能够达到的目的即可),而我们需要的是所有标签对应的数据重复数量最多的映射关系,所以我们可以在这个矩阵前加个负号,就能由求最多变成求最少,如图
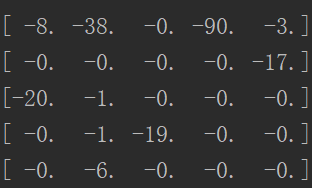
然后利用Python集成的Munkres方法计算出标签对应关系为:
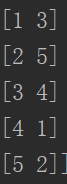
意思就是 ,预测标签为1的所有数据的标签需要改成3,以此类推。
完整代码
首先安装Munkres库,命令如下:
conda install munkres以COIL20数据集为例,该数据集是一个object datasets,由1440个samples,20个objects组成,每张图片的维度是32*32。该数据集由训练集[‘fea’]和标签集['gnd']组成。labels的数据形式为:
[ 1 1 1 ... 20 20 20]
假设聚类后的标签为:
[ 3 3 3 ... 14 14 14]
from munkres import Munkres,print_matrix
def best_map(L1,L2):
#L1 should be the labels and L2 should be the clustering number we got
Label1 = np.unique(L1) # 去除重复的元素,由小大大排列
nClass1 = len(Label1) # 标签的大小
Label2 = np.unique(L2)
nClass2 = len(Label2)
nClass = np.maximum(nClass1,nClass2)
G = np.zeros((nClass,nClass))
for i in range(nClass1):
ind_cla1 = L1 == Label1[i]
ind_cla1 = ind_cla1.astype(float)
for j in range(nClass2):
ind_cla2 = L2 == Label2[j]
ind_cla2 = ind_cla2.astype(float)
G[i,j] = np.sum(ind_cla2 * ind_cla1)
m = Munkres()
index = m.compute(-G.T)
index = np.array(index)
c = index[:,1]
newL2 = np.zeros(L2.shape)
for i in range(nClass2):
newL2[L2 == Label2[i]] = Label1[c[i]]
return newL2def err_rate(gt_s,s):
print(gt_s)
print(s)
c_x=best_map(gt_s,s)
err_x=np.sum(gt_s[:]!=c_x[:])
missrate=err_x.astype(float)/(gt_s.shape[0])
return missrate在err_rate(gt_s,s)方法中,gt_s表示真实标签数组,s表示预测标签数组。通过调用best_map(gt_s,s)方法可以得到映射后的标签,然后使用np.sum(gt_s[:]!=c_x[:])可以得到预测错误的标签个数err_x,err_x除以总的标签个数即可以得到错误率,进而可以计算聚类之后的准确率
本文由simyng创作,
采用知识共享署名4.0 国际许可协议进行许可,转载前请务必署名
文章最后更新时间为:April 18th , 2020 at 03:21 pm